基于数据分析的云计算数据中心精密空调节能控制方法与流程

基于数据分析的云计算数据中心精密空调节能控制方法
[0001]
本申请是以下原申请的分案申请：
[0002]
原申请的申请日：2020年07月15日
[0003]
原申请的申请号：202010677684.4
[0004]
原申请的发明创造名称：
[0005]
本发明涉及数据中心冷源设计领域，具体地，涉及基于数据分析的云计算数据中心精密空调节能控制方法及介质与系统。


背景技术：

[0006]
随着信息产业及社会经济的不断发展，数据中心的建设规模和数量都在高速增长。数据中心的散热量也在飞速攀升，为保证数据中心的正常运行，需全年开启精密空调系统以排出机房内数据中心所产生的热量。
[0007]
随着数据中心的竞争加剧，运营成本的压力增大，如何实现精密空调冷却系统的节能迫在眉睫。目前的精密空调冷却系统制冷方式多采用热力学的预测方法，但是热力学的预测方法计算复杂，求解过程缓慢，不能适用于实时的动态的温度预测。
[0008]
因此，需要考虑温度预测的实时性，设计一种温度预测快速算法，实时计算精密空调最优控制量，提高精密空调冷却系统的节能性，最终提升整个系统的总效率。


技术实现要素：

[0009]
针对现有技术中的缺陷，本发明的目的是提供一种基于数据分析的云计算数据中心精密空调节能控制方法及介质与系统。
[0010]
根据本发明提供的一种基于数据分析的云计算数据中心精密空调节能控制方法，包括如下步骤：
[0011]
步骤s1：利用历史上采样数据，构建初始训练数据集；定义每两个相邻采样时刻间的时段为一个采样周期，在每一个采样周期上定义一个预测周期，预测周期的长度为温差预测模型的预测深度，预测周期初始时刻为同一采样周期初始时刻；其中，将预测周期初始时刻时云服务器的热源数据、水冷精密空调的控制量数据作为模型输入数据，将同一预测周期结束时刻时的实测的传感器温差作为模型输出数据，来构建初始训练数据集；所述热源数据包括云服务器部件的性能数据与温度数据，所述控制量数据包括电动水阀开度与空调频率，所述传感器温差为水冷精密空调的回风位置温度与出风位置温度的差值；所述实测的传感器温差为水冷精密空调的实测的回风位置温度与实测的出风位置温度的差值；
[0012]
步骤s2：对所述初始训练数据集进行预处理；
[0013]
步骤s3：使用预处理后的初始训练数据，对贝叶斯线性回归模型进行初始训练，得到初始温差预测模型；
[0014]
步骤s4：获取新增训练数据集；其中，所述新增训练数据集包括：云服务器在当前
采样周期初始时刻结束的预测周期初始时刻时的热源数据、水冷精密空调在当前采样周期初始时刻结束的预测周期初始时刻时的控制量数据、机房在当前采样周期初始时刻结束的预测周期结束时刻的实测的传感器温差；
[0015]
步骤s5：对所述新增训练数据集进行预处理；
[0016]
步骤s6：使用预处理后的新增训练数据集以增量的方式，对贝叶斯线性回归模型进行在线的增量训练；
[0017]
步骤s7：基于当前的贝叶斯线性回归模型，通过预测当前采样周期上定义的预测周期结束时刻时的传感器温差，寻找电动水阀开度与空调频率的最优组合并采用实施；其中，遍历根据当前采样周期初始时刻的热源数据与档位组合集合中的各个元素作为当前贝叶斯线性回归模型的输入分别得到的当前采样周期上定义的预测周期结束时刻的预测的传感器温差，按照小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素重新设置水冷精密空调在当前采样周期内的电动水阀开度与空调频率；其中，所述档位组合集合是不同档位的电动水阀开度与不同档位的空调频率之间两两配对所得到的组合作为元素的全集；
[0018]
步骤s8：判断流程是否结束；若是，则流程结束；若否，则针对当前采样周期的下一个采样周期跳回步骤s4继续执行。
[0019]
优选地，步骤s1和步骤s4中的所述性能数据包括如下任一种或任多种数据：
[0020]-机房每台云服务器节点的风扇转速；
[0021]-机房每台云服务器节点的cpu频率；
[0022]-机房每台云服务器节点的内存使用率；
[0023]
所述温度数据包括如下任一种或任多种数据：
[0024]-机房每台云服务器节点的进风温度；
[0025]-机房每台云服务器节点的出风温度；
[0026]-机房每台云服务器节点的cpu温度；
[0027]-机房每台云服务器节点的gpu温度。
[0028]
优选地，所述步骤s2和步骤s5包括如下步骤：
[0029]
数据清洗步骤：如果在采样时刻t获得的采样数据项的值x
″
t
为空缺值，使用该数据项的历史平均值填充空缺值；
[0030]
归一化步骤：对于每一个数据项，将所述步骤s1中定义的初始训练集中数据项的最小值、最大值分别记为x
min
、x
max
，将数据项的原始值x
″
t
映射成近似在区间[0,1]中的新值x
′
t
，其公式为：
[0031][0032]
权重调整步骤：将时间较远的训练样本设定为对所述贝叶斯线性回归模型的贡献较低，贡献权重所对应的线性函数为：
[0033]
w(t)＝α(t-t0)
[0034]
其中，w(t)表示关于时间的贡献权重，α表示用来调整贡献权重w(t)随时间增长的速率的参数，t表示当前采样时刻，t0表示历史第一次采样时刻，α∈(0,+∞)；
[0035]
数据项的值x
′
t
经权重调整为新值x
t
,其公式为：
[0036]
x
t
＝w(t)x
′
t
[0037]
将训练样本中每一数据项经预处理后获得的数据项的值x
t
合并为预处理后训练样本作为步骤s3中贝叶斯线性回归初始训练和步骤s6中贝叶斯线性回归增量训练的输入。
[0038]
优选地，所述步骤s3包括：
[0039]
初始学习步骤：在贝叶斯线性回归初始训练阶段，选择模型参数先验分布服从给定初始超参数为μ0，λ0，a0，b0的高斯-反gamma概率分布，贝叶斯线性回归模型在完成初始训练后，模型参数后验分布服从超参数为μ
n
，λ
n
，a
n
，b
n
的高斯-反gamma概率分布,其中n表示初始训练数据集中的最后一个采样周期；超参数μ
n
，λ
n
，a
n
，b
n
均为μ0，λ0，a0，b0及初始训练样本集的简单函数,有解析解；
[0040]
所述步骤s6包括：
[0041]
增量学习步骤：在贝叶斯线性回归增量训练阶段，当前采样周期t之前的模型参数服从超参数为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
的高斯-反gamma概率分布，在当前采样周期t通过增添采样周期t的采样训练样本，更新当前采样周期t的模型参数为服从超参数μ
t
，λ
t
，a
t
，b
t
的高斯-反gamma概率分布；超参数μ
t
，λ
t
，a
t
，b
t
均为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
及增量训练样本的简单函数，有解析解。
[0042]
优选地，连续相邻的两个预测周期的初始时刻分别为连续相邻的两个采样周期的初始时刻。
[0043]
根据本发明提供的一种存储有计算机程序的计算机可读存储介质，所述计算机程序被处理器执行时实现所述的基于数据分析的云计算数据中心精密空调节能控制方法的步骤。
[0044]
根据本发明提供的一种基于数据分析的云计算数据中心制冷系统，包括：
[0045]
机房单元200，设置有云服务器；
[0046]
制冷区域300，设置在所述机房单元200的一侧，所述制冷区域300通过送风通道329连接所述机房单元200，所述制冷区域300产生的冷空气通过所述送风通道329进入所述机房单元200，所述制冷区域300内设置有水冷精密空调制冷单元；
[0047]
其中，所述水冷精密空调制冷单元包括：
[0048]
水冷精密空调320，对来自机房单元200的空气进行降温作业；
[0049]
电动水阀322，设置在所述水冷精密空调320的冷冻水回水管323上；
[0050]
第一传感器311，设置在所述制冷区域300内，位于所述水冷精密空调320的回风位置上，所述第一传感器311电性连接控制单元400，所述第一传感器311用于采集进入所述水冷精密空调320的热空气的温度，并将采集到的温度发送至控制单元400，所述控制单元400将所述第一传感器311发送的温度定义为回风位置温度；
[0051]
第二传感器312，设置在所述送风通道329内，位于所述水冷精密空调320的底部，所述第二传感器312电性连接控制单元400，所述第二传感器312用于采集所述水冷精密空调320输出的冷空气的温度，并将采集到的温度发送至控制单元400，控制单元400将所述第二传感器312发送的温度定义为出风位置温度。
[0052]
所述基于数据分析的云计算数据中心制冷系统还包括：
[0053]
控制单元400，所述控制单元400包括权利要求6所述的存储有计算机程序的计算机可读存储介质，以对所述水冷精密空调320的电动水阀开度与空调频率进行控制。
[0054]
优选地，在所述控制单元400中，所述存储有计算机程序的计算机可读存储介质中的程序模块包括：
[0055]
数据采集模块410：采集云服务器的热源数据、水冷精密空调的控制量数据、实测的传感器温差；
[0056]
数据预处理模块420：对数据采集模块410采集的数据进行预处理；
[0057]
温差预测模型训练模块430：使用预处理后的数据对贝叶斯线性回归模型进行训练；
[0058]
最优解搜索模块440：基于贝叶斯线性回归模型，寻找电动水阀开度与空调频率的最优组合并采用实施。
[0059]
优选地，在所述控制单元400中，
[0060]
所述数据采集模块410包括：
[0061]
初始训练数据集构建模块411：利用历史上采样数据，构建初始训练数据集；定义每两个相邻采样时刻间的时段为一个采样周期，在每一个采样周期上定义一个预测周期，预测周期的长度为温差预测模型的预测深度，预测周期初始时刻为同一采样周期初始时刻；其中，将预测周期初始时刻时云服务器的热源数据、水冷精密空调的控制量数据作为模型输入数据，将同一预测周期结束时刻时的实测的传感器温差作为模型输出数据，来构建初始训练数据集；所述热源数据包括云服务器部件的性能数据与温度数据，所述控制量数据包括电动水阀开度与空调频率，所述传感器温差为水冷精密空调的回风位置温度与出风位置温度的差值；所述实测的传感器温差为水冷精密空调的实测的回风位置温度与实测的出风位置温度的差值；
[0062]
新增训练数据集构建模块412：获取新增训练数据集；其中，所述新增训练数据集包括：云服务器在当前采样周期初始时刻结束的预测周期初始时刻时的热源数据、水冷精密空调在当前采样周期初始时刻结束的预测周期初始时刻时的控制量数据、机房在当前采样周期初始时刻结束的预测周期结束时刻的实测的传感器温差；
[0063]
所述数据预处理模块420包括：
[0064]
初始训练数据集预处理模块421：对所述初始训练数据集进行预处理；
[0065]
新增训练数据集预处理模块422：对所述新增训练数据集进行预处理；
[0066]
所述温差预测模型训练模块430包括：
[0067]
初始训练数据集训练模块431：使用预处理后的初始训练数据，对贝叶斯线性回归模型进行初始训练，得到初始温差预测模型；
[0068]
新增训练数据集训练模块432：使用预处理后的新增训练数据集以增量的方式，对贝叶斯线性回归模型进行在线的增量训练；
[0069]
所述最优解搜索模块440包括：
[0070]
网格搜索模块441：基于当前的贝叶斯线性回归模型，通过预测当前采样周期上定义的预测周期结束时刻时的传感器温差，寻找电动水阀开度与空调频率的最优组合并采用实施；其中，遍历根据当前采样周期初始时刻的热源数据与档位组合集合中的各个元素作为当前贝叶斯线性回归模型的输入分别得到的当前采样周期上定义的预测周期结束时刻的预测的传感器温差，按照小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素重新设置水冷精密空调在当前采样周期内的电动水阀开度与空调频率；其中，所述档
位组合集合是不同档位的电动水阀开度与不同档位的空调频率之间两两配对所得到的组合作为元素的全集；
[0071]
流程结束判断模块442：判断流程是否结束；若是，则流程结束；若否，则针对当前采样周期的下一个采样周期跳回触发新增训练数据集构建模块412继续执行。
[0072]
与现有技术相比，本发明具有如下的有益效果：
[0073]
1、本发明以云服务器热源数据以及精密空调控制量数据的历史数据集初始训练贝叶斯线性回归模型，用于未来时间数据中心温度传感器温差的预测，并在控制过程中实时获取新增训练数据，实时更新贝叶斯线性回归预测模型，实时预测传感器温差，并实时利用网格搜索算法获得离散的压缩机频率与水阀开度组合的最优控制量，以较小能量消耗实现未来传感器实际温差小于温差预设阈值的控制目标。
[0074]
2、本发明选择有效环境温度预测输入量，结合在线增量学习预测算法及离散网格搜索法，控制过程即训练过程，快速高效计算水冷精密空调最优控制量，最终获得很好的精密空调节能效果。
[0075]
3、本发明中的预测模型、控制量遍历以及最优控制三者之间密切相关，环环相扣，在共同作用下有效提高了节能控制的实时性。
附图说明
[0076]
通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
[0077]
图1为本发明的整体方法的步骤流程图；
[0078]
图2为本发明的整体方法中的预处理部分的步骤流程图；
[0079]
图3为本发明实施例中数据中心的结构示意图；
[0080]
图4为本发明实施例中数据中心的控制单元的控制关系示意图；
[0081]
图5为本发明实施例中水冷精密空调制冷单元的结构示意图；
[0082]
图6为本发明的控制单元的结构示意图；
[0083]
图7为本发明的控制单元的详细结构示意图。
[0084]
图中示出：
[0085]
数据中心100；
[0086]
机房单元200；
[0087]
服务器机柜201；
[0088]
墙体202；
[0089]
制冷区域300；
[0090]
第一传感器311；
[0091]
第二传感器312；
[0092]
水冷精密空调320；
[0093]
风机321；
[0094]
电动水阀322；
[0095]
冷冻水回水管323；
[0096]
冷冻水供管324；
[0097]
冷冻水循环泵325；
[0098]
螺杆压缩机326；
[0099]
蓄冷罐327；
[0100]
热风通道328；
[0101]
送风通道329；
[0102]
控制单元400；
[0103]
数据采集模块410；
[0104]
初始训练数据集构建模块411；
[0105]
新增训练数据集构建模块412；
[0106]
数据预处理模块420；
[0107]
初始训练数据集预处理模块421；
[0108]
新增训练数据集预处理模块422；
[0109]
温差预测模型训练模块430；
[0110]
初始训练数据集训练模块431；
[0111]
新增训练数据集训练模块432；
[0112]
最优解搜索模块440；
[0113]
网格搜索模块441；
[0114]
流程结束判断模块442。
具体实施方式
[0115]
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。
[0116]
需要说明的是，实施例中所提供的图示仅以示意方式说明本发明的基本构想，遂图示中仅显示与本发明中有关的组件而非按照实际实施时的组件数目、形状及尺寸绘制，其实际实施时各组件的型态、数量及比例可为一种随意的改变，且其组件布局型态也可能更为复杂。
[0117]
如图1所示，根据本发明提供的一种基于数据分析的云计算数据中心精密空调节能控制方法，包括如下步骤。
[0118]
步骤s1：利用历史上采样数据，构建初始训练数据集；定义每两个相邻采样时刻间的时段为一个采样周期，在每一个采样周期上定义一个预测周期，预测周期的长度为温差预测模型的预测深度，预测周期初始时刻为同一采样周期初始时刻，即预测周期初始时刻为预测周期被定义的采样周期的初始时刻；其中，将预测周期初始时刻时云服务器的热源数据、水冷精密空调的控制量数据作为模型输入数据，将同一预测周期结束时刻时的实测的传感器温差作为模型输出数据，来构建初始训练数据集；所述热源数据包括云服务器部件的性能数据与温度数据，所述控制量数据包括电动水阀开度与空调频率，所述传感器温差为水冷精密空调的回风位置温度与出风位置温度的差值；所述实测的传感器温差为水冷精密空调的实测的回风位置温度与实测的出风位置温度的差值。
[0119]
具体地，为提高预测的准确性，初始训练数据集中的历史上的数据为同一个云服务器数据中心单一制冷区域的历史数据，虽然云服务器数据中心可能会发生云服务器更新升级等情况，但是单个服务器更新升级基本上对于热力学过程的影响十分有限，因此使用同一个云服务器数据中心的历史数据来训练针对该云服务器数据中心的传感器温差预测模型能够提高预测准确率。
[0120]
更为具体地，在优选例中，一个预测周期由多个连续的采样周期构成，且预测周期的初始时刻与第一个采样周期的初始时刻为同一个时刻；连续相邻的两个预测周期的初始时刻分别为连续相邻的两个采样周期的初始时刻。例如，假设有十个采样时刻，记为t1,t2,
…
,t10；每一个采样时刻至下一个采样时刻之间的间隔时间构成一个采样周期，该采样周期的初始时刻即为该采样时刻，该采样周期的结束时刻即为该下一个采样时刻。进一步假设一个预测周期由五个采样周期构成，则第一个预测周期是t1至t6之间的间隔时间，第二个预测周期是t2至t7之间的间隔时间，第三个预测周期是t3至t8之间的间隔时间，以此类推。一个预测周期的初始时刻即有对应的一个采样周期的初始时刻与之同步，从而在该采样周期的初始时刻获得到的云服务器的热源数据、水冷精密空调的控制量数据这些采样数据，一方面可以用于对贝叶斯线性回归模型进行训练，另一方面还可以利用相同的采样数据对传感器温度进行预测控制，使得预测结果匹配于预测模型的训练过程。
[0121]
其中，所述性能数据包括数据：机房每台云服务器节点的风扇转速、机房每台云服务器节点的cpu频率、机房每台云服务器节点的内存使用率；所述温度数据包括数据：机房每台云服务器节点的进风温度；机房每台云服务器节点的出风温度；机房每台云服务器节点的cpu温度；机房每台云服务器节点的gpu温度。所述性能数据可以由云服务器的硬件管理程序读取cpu等设备的参数获得。所述温度数据可以由云服务器自带的温度传感器采集获得。
[0122]
步骤s2：对所述初始训练数据集进行预处理。
[0123]
如图2所示，具体地，初始训练数据集中的数据并非一定是理想的，例如存在数据遗失等问题，因此需要对初始训练数据集中的数据进行预处理，所述预处理包括如下步骤：
[0124]
数据清洗步骤：如果在采样时刻t获得的采样数据项的值x
″
t
为空缺值，使用该数据项的历史平均值填充空缺值。
[0125]
归一化步骤：对于每一个数据项，将所述步骤s1中定义的初始训练集中数据项的最小值、最大值分别记为x
min
、x
max
，将数据项的原始值x
″
t
映射成近似在区间[0,1]中的新值x
′
t
，其公式为：
[0126][0127]
权重调整步骤：将时间较远的训练样本设定为对所述贝叶斯线性回归模型的贡献较低，贡献权重所对应的线性函数为：
[0128]
w(t)＝α(t-t0)
[0129]
其中，w(t)表示关于时间的贡献权重，α表示用来调整贡献权重w(t)随时间增长的速率的参数，t表示当前采样时刻，t0表示历史第一次采样时刻，α∈(0,+∞)。
[0130]
数据项的值x
′
t
经权重调整为新值x
t
,其公式为：
[0131]
x
t
＝w(t)x
′
t
[0132]
将训练样本中每一数据项经预处理后获得的数据项的值x
t
合并为预处理后训练样本作为步骤s3中贝叶斯线性回归初始训练和步骤s6中贝叶斯线性回归增量训练的输入。
[0133]
此处考虑到了例如云服务器本身在历史上可能会发生改变，又例如云服务器中的cpu等部件在历史上也可能会因为更换而发生改变，还例如云服务器中运行的客户应用会随历史不同时段发生改变，本发明中对温度的预测模型训练用样本按时间做权重调整，时间较远的训练样本对温差预测模型的贡献度的权值较低，反之，时间较近的训练样本，对温差预测模型的贡献度的权值大。
[0134]
步骤s3：使用预处理后的初始训练数据，对贝叶斯线性回归模型进行初始训练，得到初始温差预测模型。
[0135]
具体地，所述初始温差预测模型即为初始训练后的贝叶斯线性回归模型，初始训练集作为输入提供给贝叶斯线性回归模型实现机器学习，贝叶斯线性回归模型输出的是预测的传感器温度。例如，假设机房单元中设置有320个云服务器，从每个云服务器获取3种性能数据和4种温度数据，以及水冷精密空调的水阀开度与空调频率作为贝叶斯线性回归模型的输入，贝叶斯线性回归模型输出的是预测的传感器温差。
[0136]
更为具体地，在温度变化预测中，通过使用贝叶斯线性回归模型进行统计推理，通过选择高斯-反gamma概率分布作为贝叶斯线性回归模型参数共轭先验分布，利用初始训练数据进行贝叶斯推理所获得贝叶斯线性回归模型参数的后验分布亦为高斯-反gamma概率分布。贝叶斯线性回归模型参数的先验分布与后验分布为同分布，这使得步骤s6的贝叶斯线性回归模型在线快速增量训练成为可能，从而达到快速高效精准预测温差的目的。
[0137]
下面对所述贝叶斯线性回归模型进行详细说明。
[0138]
即，贝叶斯线性回归模型的输入样本集合x由n个连续采样周期输入样本组成，这里采用记号：x＝{x1,x2,...,x
n
}。x为矩阵表达形式。x
n
表示在第n个采样周期获得的输入样本，在本发明应用实例中输入样本数据包括云服务器的热源数据、水冷精密空调的控制量数据。贝叶斯线性回归模型输出样本集合y由n个连续采样周期输出样本组成，这里采用记号：y＝{y1,y2,...,y
n
}。y
n
表示在第n个采样周期获得的输出样本，在本发明应用实例中输出样本为实测的传感器温差数据。
[0139]
所述贝叶斯线性回归模型如下：
[0140][0141]
ρ(y|x,β,σ2)表示在给定输入样本集合x，贝叶斯线性回归模型参数β和σ2下，输出样本集合y的条件概率密度函数。如上式所述，输出样本集合y的条件概率服从n维高斯分布。
[0142]
其中β为输入样本特征的权重向量。
[0143]
σ2为线性回归残差的方差；β，σ2即构成贝叶斯线性回归模型的参数。
[0144]
接下来对贝叶斯线性回归模型参数β和σ2的先验概率分布进行展开说明。依据贝叶斯推理原理，共轭先验概率ρ(β,σ2)可以分解为ρ(β,σ2)＝ρ(σ2)ρ(β|σ2)，选用超参数为μ0，λ0，a0，b0的高斯-反gamma概率分布作为参数β和σ2的先验概率分布。其中方差σ2的概率密度函数形式如下式：
[0145][0146]
方差σ2服从反gamma(a0,b0)分布；参数a0和b0为反gamma分布的超参数；在本发明应用实例中超参数值的选择为a0＝1，b0＝1。
[0147]
给定方差σ2，权重向量β的条件概率密度函数形式如下式：
[0148][0149]
给定方差σ2，β服从高斯分布；期望向量μ0，方差矩阵λ0为k维高斯分布的超参数；在本发明应用实例中超参数值的选择：
[0150]
μ0为k维0向量；参数λ0表示k
×
k阶单位矩阵；k表示作为输入量的输入样本集合x的特征维度。
[0151]
接着对模型参数β和σ2的后验概率分布进行展开说明。
[0152]
模型参数的后验分布由下式计算：
[0153][0154]
其中，ρ(β,σ2|y,x)是给定输入样本集合x和输出样本集合y时的模型参数的后验概率密度函数。后验概率密度等于输出的似然ρ(y|x,β,σ2)乘以给定输入的参数β,σ2的先验概率密度函数ρ(β,σ2)并且除以归一化常数。
[0155]
具体到贝叶斯线性回归，后验分布为：
[0156][0157]
其中ρ(β|σ2,y,x)为高斯分布的密度函数；
[0158]
ρ(σ2|y,x)为反-gamma(a
n
,b
n
)分布的密度函数；
[0159]
综上所述，即模型在观测到输入样本集x和输出样本集y后，参数β和σ2的后验概率
分布服从超参数为μ
n
，λ
n
，a
n
，b
n
的高斯-反gamma分布，超参数的计算公式如下：
[0160]
μ
n
＝(x
t
x+λ0)-1
(λ0μ0+x
t
y)
[0161]
λ
n
＝(x
t
x+λ0)
[0162][0163][0164]
参数μ
n
为高斯分布的期望向量；
[0165]
参数为分布的方差矩阵；
[0166]
a
n
，b
n
为反-gamma(a
n
,b
n
)分布的超参数。
[0167]
经过上述贝叶斯统计推理，贝叶斯线性回归输入特征权重参数β的初始训练最优贝叶斯估计为：
[0168][0169]
使用初始贝叶斯最优线性回归模型对预测周期m结束时刻传感器温差的预测值表示为其中表示预测周期m结束时刻的传感器温差的预测值,x
m
表示预测周期m开始时刻的输入性能数据和温度数据。
[0170]
步骤s4：获取新增训练数据集；其中，所述新增训练数据集包括：云服务器在当前采样周期初始时刻结束的预测周期初始时刻时的热源数据、水冷精密空调在当前采样周期初始时刻结束的预测周期初始时刻时的控制量数据、机房在当前采样周期初始时刻结束的预测周期结束时刻的实测的传感器温差；
[0171]
步骤s5：对所述新增训练数据集按步骤s2相同方式进行预处理；即，对所述新增训练数据集进行预处理的实施可参照图2的步骤具体实现。
[0172]
步骤s6：使用预处理后的新增训练数据集以增量的方式，对贝叶斯线性回归模型进行在线的增量训练；
[0173]
具体地，本发明采用在线实时更新温差预测模型，控制过程即训练过程，实时预测传感器温差。所述步骤s6包括增量学习步骤：设当前增量训练对应的预测周期为t,预测周期初始时刻前贝叶斯线性回归模型参数β,σ2服从超参数为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
的高斯-反gamma概率分布，在当前预测周期t通过增添预测周期t初始时刻的采样训练样本，更新当前预测周期t的模型参数为服从超参数μ
t
，λ
t
，a
t
，b
t
的高斯-反gamma概率分布。超参数μ
t
，λ
t
，a
t
，b
t
均为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
及增量训练样本的简单函数，有解析解，计算快捷，从而实现在线的快速增量训练。在本发明应用实例中，采样周期设为30秒。在计算资源充足的情况下，每一次贝叶斯线性回归模型增量训练预测及输出控制指令的耗时非常短(低于1秒)，完全可以满足水冷精密空调实时在线控制的设计目标。
[0174]
接下来就贝叶斯线性回归增量训练进行详细说明。
[0175]
在输入样本数n>1的情况下，贝叶斯增量训练以下式表示：
[0176]
ρ(β,σ2|y
1,
…
,t
,x
1,
…
,t
)
∝
ρ(y
t
|x
t
,β,σ2)
×
ρ(β,σ2|y
1,
…
,t-1
,x
1,
…
,t-1
)
[0177]
其中，ρ(β,σ2|y
1,
…
,t
,x
1,
…
,t
)为在采样周期t观测到所有历史输入样本集合x
1,
…
,t
和所有历史输出样本集合y
1,
…
,t
的条件下模型参数β,σ2的概率密度函数。此项等于给定当前采
样周期输入样本x
t
，当前采样周期输出样本y
t
的似然ρ(y
n
|x
n
,β,σ2)乘以在采样周期n-1中观测到所有历史输入样本集合x
1,
…
,t-1
和所有历史输出样本集合y
1,
…
,t-1
的条件下模型参数β,σ2的概率密度函数ρ(β,σ2|y
1,
…
,n-1
,x
1,
…
,n-1
)并归一化。
[0178]
具体到贝叶斯线性回归,设在采样周期t-1时，模型参数β,σ2的后验概率密度函数为超参数为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
的高斯-反gamma分布，在采样周期t，观测到新的训练样本x
t
，y
t
后，模型参数β,σ2的后验概率密度函数为超参数为μ
t
，λ
t
，a
t
，b
t
的高斯-反gamma分布。超参数更新公式即增量训练公式如下：
[0179]
μ
t
＝(x
tt
x
t
+λ
t-1
)-1
(λ
t-1
μ
t-1
+x
tt
y
t
)
[0180]
λ
t
＝(x
tt
x
t
+λ
t-1
)
[0181][0182][0183]
经过上述贝叶斯统计推理，在当前采样周期t内，贝叶斯线性回归输入特征权重参数β的增量训练最优贝叶斯估计为：
[0184][0185]
使用当前增量贝叶斯最优线性回归模型对当前预测周期t结束时刻传感器温差的预测由公式1表示：
[0186][0187]
其中表示当前预测周期t结束时刻的传感器温差的预测值,x
t
表示当前预测周期t开始时刻的模型输入的性能数据和温度数据。
[0188]
步骤s7：基于当前的贝叶斯线性回归模型，通过使用步骤s6的公式1预测当前采样周期上定义的预测周期结束时刻时的传感器温差，寻找电动水阀开度与空调频率的最优组合并采用实施；其中，遍历根据当前采样周期初始时刻的热源数据与档位组合集合中的各个元素作为当前贝叶斯线性回归模型的输入分别得到的当前采样周期初始时刻起一个预测周期结束时的预测的传感器温差，按照小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素重新设置水冷精密空调在当前采样周期内的电动水阀开度与空调频率；其中，所述档位组合集合是不同档位的电动水阀开度与不同档位的空调频率之间两两配对所得到的组合作为元素的全集；
[0189]
具体地，本发明实时利用网格搜索算法获得离散的压缩机频率与水阀开度组合的最优控制量，以较小能量消耗实现未来传感器实际温差小于温差预设阈值的控制目标。所述步骤s10包括网格搜索步骤：通过网格搜索算法，根据所述热源数据与档位组合集合中的各个元素作为模型输入得到小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素；其中，所述电动水阀开度的档位、空调频率的档位，均为离散档位。
[0190]
更为具体地，可以设置机房中水冷精密空调的电动水阀开度和空调频率为离散挡位数，且档位总计数量不多，然后进一步使用网格搜索算法，获取最优解，即临近目标温差阈值的最小的电动水阀开度和最低空调频率的组合，其中，空调频率是水冷精密空调的风机频率。例如，设定电动水阀开度共有m档，m的值可取10，空调频率共n档，n的值可取20，则
根据网格搜索算法，枚举出m*n种参数组合方式，在集合(m,n)参数对中，将参数对输入到作为温差预测模型的当前贝叶斯线性回归模型中，遍历循环所有值的排列组合结果，将预测的温差结果大于等于目标温差阀值的结果值进行剔除，同时找到低于并最接近目标温差阈值的预测的传感器温差所对应的电动水阀开度与风机频率组合，作为最优解控制量，使用此最优解控制量作为电动水阀和风机频率作为水冷精密空调的控制输入控制量。其中，由于仅有20乘以10等于200个网格，因此计算时间可忽略不计，对贝叶斯线性回归模型训练的实时性要求不会产生影响。
[0191]
步骤s8：判断流程是否结束；若是，则流程结束；若否，则针对当前采样周期的下一个采样周期跳回步骤s4继续执行。
[0192]
接下来结合更多的附图基于作为优选例的数据中心100的实施例，对本发明提供的基于数据分析的云计算数据中心制冷系统进行详细的说明。
[0193]
如图3所示，在本实施例中，数据中心100包括基于数据分析的云计算数据中心制冷系统。其中，所述基于数据分析的云计算数据中心制冷系统包括机房单元200、制冷区域300。制冷区域300位于机房单元200的一侧，制冷区域300为机房单元200提供冷气。
[0194]
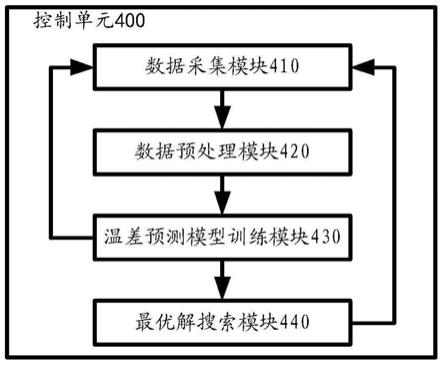
如图4所示，所述基于数据分析的云计算数据中心制冷系统还包括控制单元400。控制单元400对机房单元200和制冷区域300中的装置进行数据采集与控制。所述控制单元400包括存储有计算机程序的计算机可读存储介质，以对所述水冷精密空调320的电动水阀开度与空调频率进行控制。
[0195]
如图5所示，在本实施例中，机房单元200，设置有云服务器；
[0196]
制冷区域300，设置在所述机房单元200的一侧，所述制冷区域300通过送风通道329连接所述机房单元200，所述制冷区域300产生的冷空气通过所述送风通道329进入所述机房单元200，所述制冷区域300内设置有水冷精密空调制冷单元；
[0197]
其中，所述水冷精密空调制冷单元包括：
[0198]
水冷精密空调320，对来自机房单元200的空气进行降温作业；
[0199]
电动水阀322，设置在所述水冷精密空调320的冷冻水回水管323上；
[0200]
第一传感器311，设置在所述制冷区域300内，位于所述水冷精密空调320的回风位置上，所述第一传感器311电性连接控制单元400，所述第一传感器311用于采集进入所述水冷精密空调320的热空气的温度，并将采集到的温度发送至控制单元400，所述控制单元400将所述第一传感器311发送的温度定义为回风位置温度；
[0201]
第二传感器312，设置在所述送风通道329内，位于所述水冷精密空调320的底部，所述第二传感器312电性连接控制单元400，所述第二传感器312用于采集所述水冷精密空调320输出的冷空气的温度，并将采集到的温度发送至控制单元400，控制单元400将所述第二传感器312发送的温度定义为出风位置温度。
[0202]
进一步更为具体地，该制冷区域300设置在机房单元200的一侧，该机房单元200包括服务器机柜201和墙体202，服务器机柜201设置在机房单元200内，通过墙体202将机房单元200和制冷区域300隔开，并且墙体202上设置有连通机房单元200和制冷区域300的热风通道328。在本实施例中，该机房单元200内可包括至少两列服务器机柜201，两列服务器机柜201可以背靠背设置，每列服务器机柜201内至少包括若干个服务器。相邻两列服务器机柜201之间形成热通道，即服务器机柜201产生的热量从热通道内流出，通过热风通道328以
进入制冷区域300。
[0203]
在本实施例中，第一传感器311、第二传感器312均电性连接至控制单元400。如图5所示，第一传感器311设置在制冷区域300内，位于水冷精密空调320的回风位置上。第二传感器312设置在送风通道329内，且位于水冷精密空调320的下方。
[0204]
如图5所示，水冷精密空调制冷单元包括水冷精密空调320、风机321、电动水阀322、冷冻水循环泵325、螺杆压缩机326和蓄冷罐327。在本实施例中，该水冷精密空调320通过冷冻水回水管323和冷冻水循环泵325连接，然后和螺杆压缩机326连接，螺杆压缩机326连接蓄冷罐327，蓄冷罐327通过冷冻水供管324连接水冷精密空调320，水冷精密空调320、冷冻水循环泵325、螺杆压缩机326和蓄冷罐327形成循环水路。制冷区域300形成的冷气通过送风通道329进入机房单元200内。
[0205]
如图6所示，在优选例中，所述控制单元所包括的存储有计算机程序的计算机可读存储介质中相应的程序模块具体如下，即所述控制单元包括一种基于数据分析的云计算数据中心精密空调节能控制系统，包括如下模块：
[0206]
数据采集模块410：采集云服务器的热源数据、水冷精密空调的控制量数据、实测的传感器温差；
[0207]
数据预处理模块420：对数据采集模块410采集的数据进行预处理；
[0208]
温差预测模型训练模块430：使用预处理后的数据对贝叶斯线性回归模型进行训练；
[0209]
最优解搜索模块440：基于贝叶斯线性回归模型，寻找电动水阀开度与空调频率的最优组合并采用实施
[0210]
在实施贝叶斯线性回归预测传感器温差的初始阶段训练阶段，首先，数据采集模块410采集历史云服务器的热源数据、水冷精密空调的控制量数据、实测的传感器温差；并将采集到的历史数据发送给数据预处理模块420进行数据预处理；其次，数据预处理模块420对数据采集模块410采集的数据进行预处理；将预处理后的数据发送给温差预测模型训练模块430做贝叶斯线性回归模型的初始训练；最后，温差预测模型训练模块430使用数据预处理模块420产生的预处理后的数据对贝叶斯线性回归模型进行初始训练，获得初始贝叶斯线性回归预测模型。
[0211]
在实施贝叶斯线性回归在线增量训练、最优控制量搜索及控制阶段，在每个贝叶斯线性回归在线增量训练、最优控制量搜索及控制实施周期，首先，数据采集模块410采集当前采样周期初始时刻结束的预测周期的云服务器的热源数据、水冷精密空调的控制量数据、实测的传感器温差作为增量训练样本；并将采集到的增量训练数据发送给数据预处理模块420进行数据预处理；其次，数据预处理模块420对数据采集模块410采集的增量训练样本进行预处理；将预处理后的增量训练样本发送给温差预测模型训练模块430做贝叶斯线性回归模型的增量训练；再其次，温差预测模型训练模块430使用数据预处理模块420产生的预处理后的增量样本对贝叶斯线性回归模型进行增量训练，更新贝叶斯线性回归预测模型，并触发最优解搜索模块440；最优解搜索模块440基于最新更新的贝叶斯线性回归模型，寻找电动水阀开度与空调频率的最优组合并采用实施；最优解搜索模块440工作结束自动触发数据采集模块410采集工作开始下一个贝叶斯线性回归在线增量训练、最优控制量搜索及控制实施周期。
[0212]
如图7所示，所述数据采集模块410包括初始训练数据集构建模块411、新增训练数据集构建模块412。
[0213]
所述数据预处理模块420包括初始训练数据集预处理模块421、新增训练数据集预处理模块422。
[0214]
所述温差预测模型训练模块430包括初始训练数据集训练模块431、新增训练数据集训练模块432。
[0215]
所述最优解搜索模块440包括网格搜索模块441、流程结束判断模块442。
[0216]
初始训练数据集构建模块411：利用历史上采样数据，构建初始训练数据集；定义每两个相邻采样时刻间的时段为一个采样周期，在每一个采样周期上定义一个预测周期，预测周期的长度为温差预测模型的预测深度，预测周期初始时刻为同一采样周期初始时刻，即预测周期初始时刻为预测周期被定义的采样周期的初始时刻；其中，将预测周期初始时刻时云服务器的热源数据、水冷精密空调的控制量数据作为模型输入数据，将同一预测周期结束时刻时的实测的传感器温差作为模型输出数据，来构建初始训练数据集；所述热源数据包括云服务器部件的性能数据与温度数据，所述控制量数据包括电动水阀开度与空调频率，所述传感器温差为水冷精密空调的回风位置温度与出风位置温度的差值；所述实测的传感器温差为水冷精密空调的实测的回风位置温度与实测的出风位置温度的差值；初始训练数据集构建模块411将已构建的初始训练数据集发送给初始训练数据集预处理模块421进一步处理；
[0217]
初始训练数据集预处理模块421：对所述初始训练数据集进行预处理；然后将预处理后的初始训练数据提供给初始训练数据集训练模块431进行模型训练；
[0218]
初始训练数据集训练模块431：使用预处理后的初始训练数据，对贝叶斯线性回归模型进行初始训练，得到初始温差预测模型；
[0219]
具体地，所述初始温差预测模型即为初始训练后的贝叶斯线性回归模型，初始训练集作为输入提供给贝叶斯线性回归模型实现机器学习，贝叶斯线性回归模型输出的是预测的传感器温度。例如，假设机房单元中设置有320个云服务器，从每个云服务器获取3种性能数据和4种温度数据，以及水冷精密空调的水阀开度与空调频率作为贝叶斯线性回归模型的输入，贝叶斯线性回归模型输出的是预测的传感器温差。
[0220]
更为具体地，在温度变化预测中，通过使用贝叶斯线性回归模型进行统计推理，通过选择高斯-反gamma概率分布作为贝叶斯线性回归模型参数共轭先验分布，利用初始训练数据进行贝叶斯推理所获得贝叶斯线性回归模型参数的后验分布亦为高斯-反gamma概率分布。贝叶斯线性回归模型参数的先验分布与后验分布为同分布，这使得贝叶斯线性回归模型在线快速增量训练成为可能，从而达到快速高效精准预测温差的目的。
[0221]
下面对所述贝叶斯线性回归模型进行详细说明。
[0222]
即，贝叶斯线性回归模型的输入样本集合x由n个连续采样周期输入样本组成，这里采用记号：x＝{x1,x2,...,x
n
}。x为矩阵表达形式。x
n
表示在第n个采样周期获得的输入样本，在本发明应用实例中输入样本数据包括云服务器的热源数据、水冷精密空调的控制量数据。贝叶斯线性回归模型输出样本集合y由n个连续采样周期输出样本组成，这里采用记号：y＝{y1,y2,...,y
n
}。y
n
表示在第n个采样周期获得的输出样本，在本发明应用实例中输出样本为实测的传感器温差数据。
[0223]
所述贝叶斯线性回归模型如下：
[0224][0225]
ρ(y|x,β,σ2)表示在给定输入样本集合x，贝叶斯线性回归模型参数β和σ2下，输出样本集合y的条件概率密度函数。如上式所述，输出样本集合y的条件概率服从n维高斯分布。
[0226]
其中β为输入样本特征的权重向量；
[0227]
σ2为线性回归残差的方差；β，σ2即构成贝叶斯线性回归模型的参数。
[0228]
接下来对贝叶斯线性回归模型参数β和σ2的先验概率分布进行展开说明。依据贝叶斯推理原理，共轭先验概率ρ(β,σ2)可以分解为ρ(β,σ2)＝ρ(σ2)ρ(β|σ2)，选用超参数为μ0，λ0，a0，b0的高斯-反gamma概率分布作为参数β和σ2的先验概率分布。其中方差σ2的概率密度函数形式如下式
[0229][0230]
方差σ2服从反gamma(a0,b0)分布；参数a0和b0为反gamma分布的超参数；在本发明应用实例中超参数值的选择为a0＝1，b0＝1。
[0231]
给定方差σ2，权重向量β的条件概率密度函数形式如下式
[0232][0233]
给定方差σ2，β服从高斯分布；期望向量μ0，方差矩阵λ0为k维高斯分布的超参数；在本发明应用实例中超参数值的选择：
[0234]
μ0为k维0向量；参数λ0表示k
×
k阶单位矩阵；k表示作为输入量的输入样本集合x的特征维度。
[0235]
接着对模型参数β和σ2的后验概率分布进行展开说明。
[0236]
模型参数的后验分布由下式计算：
[0237][0238]
其中，ρ(β,σ2|y,x)是给定输入样本集合x和输出样本集合y时的模型参数的后验概率密度函数。后验概率密度等于输出的似然ρ(y|x,β,σ2)乘以给定输入的参数β,σ2的先验概率密度函数ρ(β,σ2)并且除以归一化常数。
[0239]
具体到贝叶斯线性回归，后验分布为：
[0240][0241]
其中ρ(β|σ2,y,x)为高斯分布的密度函数；
[0242]
ρ(σ2|y,x)为反-gamma(a
n
,b
n
)分布的密度函数；
[0243]
综上所述，即模型在观测到输入样本集x和输出样本集y后，参数β和σ2的后验概率分布服从超参数为μ
n
，λ
n
，a
n
，b
n
的高斯-反gamma分布，超参数的计算公式如下
[0244]
μ
n
＝(x
t
x+λ0)-1
(λ0μ0+x
t
y)
[0245]
λ
n
＝(x
t
x+λ0)
[0246][0247][0248]
参数μ
n
为高斯分布的期望向量；
[0249]
参数为分布的方差矩阵；
[0250]
a
n
，b
n
为反-gamma(a
n
,b
n
)分布的超参数。
[0251]
经过上述贝叶斯统计推理，贝叶斯线性回归输入特征权重参数β的初始训练最优贝叶斯估计为
[0252][0253]
使用初始贝叶斯最优线性回归模型对预测周期m结束时刻传感器温差的预测值表示为其中表示预测周期m结束时刻的传感器温差的预测值,x
m
表示预测周期m开始时刻的输入性能数据和温度数据。
[0254]
得到初始温差预测模型之后，系统进入贝叶斯线性回归在线增量训练、最优控制量搜索及控制阶段，在首个贝叶斯线性回归在线增量训练、最优控制量搜索及控制实施周期，初始训练数据集训练模块431触发新增训练数据集构建模块412采集新增训练数据；
[0255]
新增训练数据集构建模块412：获取新增训练数据集；其中，所述新增训练数据集包括：云服务器在当前采样周期初始时刻结束的预测周期初始时刻时的热源数据、水冷精密空调在当前采样周期初始时刻结束的预测周期初始时刻时的控制量数据、机房在当前采样周期初始时刻结束的预测周期结束时刻的实测的传感器温差；然后，新增训练数据集构建模块412将获取的新增训练数据集发送给新增训练数据集预处理模块422；
[0256]
新增训练数据集预处理模块422：对所述新增训练数据集进行预处理，并将得到的预处理后的新增训练数据集提供给新增训练数据集训练模块432进行模型的增量训练；
[0257]
新增训练数据集训练模块432：使用预处理后的新增训练数据集以增量的方式，对贝叶斯线性回归模型进行在线的增量训练；
[0258]
具体地，本发明采用在线实时更新温差预测模型，控制过程即训练过程，实时预测传感器温差。所述新增训练数据集训练模块432包括增量学习模块：设当前增量训练对应的预测周期为t,预测周期初始时刻前贝叶斯线性回归模型参数β,σ2服从超参数为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
的高斯-反gamma概率分布，在当前预测周期t通过增添预测周期t初始时刻的采样训练样本，更新当前预测周期t的模型参数为服从超参数μ
t
，λ
t
，a
t
，b
t
的高斯-反gamma概率分布。超参数μ
t
，λ
t
，a
t
，b
t
均为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
及增量训练样本的简单函数，有解析解，计算快捷，从而实现在线的快速增量训练。在本发明应用实例中，采样周期设为30秒。在计算资源充足的情况下，每一次贝叶斯线性回归模型增量训练预测及输出控制指令的耗时非常短(低于1秒)，完全可以满足水冷精密空调实时在线控制的设计目标。
[0259]
接下来就贝叶斯线性回归增量训练进行详细说明。
[0260]
在输入样本数n>1的情况下，贝叶斯增量训练以下式表示：
[0261]
ρ(β,σ2|y
1,
…
,t
,x
1,
…
,t
)
∝
ρ(y
t
|x
t
,β,σ2)
×
ρ(β,σ2|y
1,
…
,t-1
,x
1,
…
,t-1
)
[0262]
其中，ρ(β,σ2|y
1,
…
,t
,x
1,
…
,t
)为在采样周期t观测到所有历史输入样本集合x
1,
…
,t
和所有历史输出样本集合y
1,
…
,t
的条件下模型参数β,σ2的概率密度函数。此项等于给定当前采样周期输入样本x
t
，当前采样周期输出样本y
t
的似然ρ(y
n
|x
n
,β,σ2)乘以在采样周期n-1中观测到所有历史输入样本集合x
1,
…
,t-1
和所有历史输出样本集合y
1,
…
,t-1
的条件下模型参数β,σ2的概率密度函数ρ(β,σ2|y
1,
…
,n-1
,x
1,
…
,n-1
)并归一化。
[0263]
具体到贝叶斯线性回归,设在采样周期t-1时，模型参数β,σ2的后验概率密度函数为超参数为μ
t-1
，λ
t-1
，a
t-1
，b
t-1
的高斯-反gamma分布，在采样周期t，观测到新的训练样本x
t
，y
t
后，模型参数β,σ2的后验概率密度函数为超参数为μ
t
，λ
t
，a
t
，b
t
的高斯-反gamma分布。超参数更新公式即增量训练公式如下：
[0264]
μ
t
＝(x
tt
x
t
+λ
t-1
)-1
(λ
t-1
μ
t-1
+x
tt
y
t
)
[0265]
λ
t
＝(x
tt
x
t
+λ
t-1
)
[0266][0267][0268]
经过上述贝叶斯统计推理，在当前采样周期t内，贝叶斯线性回归输入特征权重参数β的增量训练最优贝叶斯估计为
[0269]
[0270]
使用当前增量贝叶斯最优线性回归模型对当前预测周期t结束时刻传感器温差的预测由公式1表示：
[0271][0272]
其中表示当前预测周期t结束时刻的传感器温差的预测值,x
t
表示当前预测周期t开始时刻的模型输入的性能数据和温度数据。
[0273]
使用预处理后的新增训练数据集以增量的方式，对贝叶斯线性回归模型进行在线的增量训练之后，新增训练数据集训练模块432触发网格搜索模块441继续处理；
[0274]
网格搜索模块441：基于当前的贝叶斯线性回归模型，通过使用新增训练数据集训练模块432中的公式1预测当前采样周期上定义的预测周期结束时刻时的传感器温差，寻找电动水阀开度与空调频率的最优组合并采用实施；其中，遍历根据当前采样周期初始时刻的热源数据与档位组合集合中的各个元素作为当前贝叶斯线性回归模型的输入分别得到的当前采样周期上定义的预测周期结束时刻的预测的传感器温差，按照小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素重新设置水冷精密空调在当前采样周期内的电动水阀开度与空调频率；其中，所述档位组合集合是不同档位的电动水阀开度与不同档位的空调频率之间两两配对所得到的组合作为元素的全集；然后，触发流程结束判断模块442判断流程是否结束；
[0275]
流程结束判断模块442：判断流程是否结束；若是，则流程结束；若否，则系统进入下一个贝叶斯线性回归在线增量训练、最优控制量搜索及控制周期，针对当前采样周期的下一个采样周期跳回触发新增训练数据集构建模块412继续执行采集新增训练数据。
[0276]
进一步地，初始训练数据集构建模块411和新增训练数据集构建模块412中的所述性能数据包括如下任一种或任多种数据：
[0277]-机房每台云服务器节点的风扇转速；
[0278]-机房每台云服务器节点的cpu频率；
[0279]-机房每台云服务器节点的内存使用率；
[0280]
所述温度数据包括如下任一种或任多种数据：
[0281]-机房每台云服务器节点的进风温度；
[0282]-机房每台云服务器节点的出风温度；
[0283]-机房每台云服务器节点的cpu温度；
[0284]-机房每台云服务器节点的gpu温度。
[0285]
进一步地，所述初始训练数据集预处理模块421和新增训练数据集预处理模块422包括如下模块：
[0286]
数据清洗模块：如果在采样时刻t获得的采样数据项的值x
″
t
为空缺值，使用该数据项的历史平均值填充空缺值；
[0287]
归一化模块：对于每一个数据项，将所述初始训练数据集构建模块411中定义的初始训练集中数据项的最小值、最大值分别记为x
min
、x
max
，将数据项的原始值x
″
t
映射成近似在区间[0,1]中的新值x
′
t
，其公式为：
[0288]
[0289]
权重调整模块：将时间较远的训练样本设定为对所述贝叶斯线性回归模型的贡献较低，贡献权重所对应的线性函数为：
[0290]
w(t)＝α(t-t0)
[0291]
其中，w(t)表示关于时间的贡献权重，α表示用来调整贡献权重w(t)随时间增长的速率的参数，t表示当前采样时刻，t0表示历史第一次采样时刻，α∈(0,+∞)；
[0292]
数据项的值x
′
t
经权重调整为新值x
t
,其公式为：
[0293]
x
t
＝w(t)x
′
t
[0294]
将训练样本中每一数据项经预处理后获得的数据项的值x
t
合并为预处理后训练样本作为初始训练数据集训练模块431中贝叶斯线性回归初始训练和新增训练数据集训练模块432中贝叶斯线性回归增量训练的输入。
[0295]
进一步地，所述初始训练数据集训练模块431包括：
[0296]
初始学习模块：选择高斯-反gamma先验概率分布，贝叶斯线性回归模型在完成初始训练后即能够进行在线的增量训练。
[0297]
所述新增训练数据集训练模块432包括：
[0298]
增量学习模块：选择高斯-反gamma先验概率分布，贝叶斯线性回归模型在完成初始训练后即能够进行在线的增量训练。
[0299]
进一步地，所述初始训练数据集构建模块4110包括：
[0300]
网格搜索模块：通过网格搜索算法，根据所述热源数据与档位组合集合中的各个元素得到小于且最接近所述目标温差阈值的预测的传感器温差所对应的元素；其中，所述电动水阀开度的档位、空调频率的档位，均为离散档位。
[0301]
进一步地，一个预测周期由多个连续的采样周期构成，且预测周期的初始时刻与第一个采样周期的初始时刻为同一个时刻；连续相邻的两个预测周期的初始时刻分别为连续相邻的两个采样周期的初始时刻。
[0302]
本领域技术人员，可以将所述基于数据分析的云计算数据中心精密空调节能控制方法理解为所述基于数据分析的云计算数据中心精密空调节能控制系统的一个具体实施例，即所述基于数据分析的云计算数据中心精密空调节能控制系统可以通过执行所述基于数据分析的云计算数据中心精密空调节能控制方法的步骤流程实现。本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的基于数据分析的云计算数据中心制冷系统中的各个程序模块以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的各个程序模块以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同程序。所以，本发明提供的各个程序模块可以被认为是一种硬件部件，而对其内包括的用于实现各种程序的子程序模块也可以视为硬件部件内的结构；也可以将用于实现各种功能的模块视为既可以是实现方法的软件程序又可以是硬件部件内的结构。
[0303]
以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本申请的实施例和实施例中的特征可以任意相互组合。

如果您还有其他的疑问和需求，请点击【立即咨询】或者是添加微信号 【13608176338】和我们鱼爪商标网客服取得联系，为你排忧解难! 此文章来源于网络,如有侵权,请联系删除

此文章来源于网络,如有侵权,请联系删除